Diversity principle and compatibility concept

If we want to model psychological and social phenomena, we have to be sure that our models have the basic properties of systems to be modeled. Psychiatric phenomena are the result of events both inside a person’s body and inside the social environment of this person. However, an analysis using hierarchical levels is often not very effective, as we cannot draw conclusions based only upon the macro level, and it is pragmatically impossible to register all activity on the micro level. From this point of view modeling of the interactions within a specific organization using multi-agent models will help to clarify the strategies of this organization and allow us to conduct a proper analysis of its dynamics.

Random graph theory, percolation models, interacting particle systems, spin glasses, cellular automata, and random boolean networks all constitute models of interacting multi-agent populations. However these models do not solve the diversity problem: real systems, and organizations generally possess a large diversity among their agents, and only diverse elements can create a system. Most models however consider formal populations with identical elements or possessing only a small diversity of types, strategies or rules.

The compatibility concept was introduced in simulations of the interactions of diverse agents (in contrast to the usual models involving homogeneous populations of agents). If we take all traits and characteristics that describe the «interests» of the agents and if we order the vector space of these traits, we could imagine the complete vector, which characterizes a certain agent within the space of these interests. Such characteristics need to be interpreted broadly and may be economical, physical, psychological, social, aesthetic, intellectual, or informational.

Every agent has such a «summarized» individuality and «motivation» and so we could compare them using only this one parameter. Such a compatibility is easy to operate with in mathematical operations and modeling, and it permits us to define a distance between each two «individuals» quantitatively. We do not even need to know the exact nature of each «interest» or trait, which corresponds to some vector. We need know only the size of the group or organization, the number of traits, in which space the differences between member of a group could be analyzed (dimension of the vector space of individual differences), and the distribution of the different types in the group. Usually we take a Gaussian distribution or uniform distribution, but if the group or organization has more specific characteristics, it is possible to change the distribution of types in the model. From this, we could determine the quantitative difference between two agents, which can be used to determine the behavioral strategy that the agents use in their connections. Thus the compatibility concept helps to reduce the difficulties connected with the modeling of the activity of a system with a diversity of elements.

We have to note that compatibility does not mean complete similarity of the agents; it is the result of the «synchronicity» of their interests, and the effectiveness of their interaction. It summaries all factors, useful and useless, of the interaction which allow the agents to receive some progress (positive compatibility) or distraction (negative compatibility) from the interaction.

We applied this concept in the «Compatibility» model (Trofimova, Potapov & Sulis, 1998) which considers different populations of agents possessing an abstract set of characteristics, which seek to form connections with other agents according to the degree of compatibility between these characteristics. Each connection carries with it a relative valuation on the part of the agent forming it, and the agents attempt to optimize their valuations over time.

This model uses another concept and corresponding parameter, so let’s explain it first before we talk about the results.

The concept of Sociability and non-locality principle

At every step an agent can hold or establish several connections, and the limit on the number of such connections gives us the parameter of an agent’s sociability. Generally sociability is the characteristic of an agent which describes the structure of its connections inside a population (maximum number of connections that it can hold, and the distribution of connections). Such a structure usually defines the behavior and functional specialization of an element inside a population, a system or a group. In the Compatibility model we considered the situation in which the distribution of connections is uniform throughout the population: every element can potentially establish contact with every other agent with equal probability. We termed such types of models having a flexible structure of connections, and with different types of probability distributions for contacts «Ensembles with Variable Structure» (EVS). Four main models were developed within the EVS approach: Compatibility model (Trofimova, Potapov & Sulis, 1998), Adaptation model (Trofimova, Mitin, Potapov, Malinetzky, 1997b), FD (Functional Differentiation) model (Trofimova, 1997a), and Resource model (Trofimova, Mitin, 1998).

The first principle of the EVS approach, as indicated above is that all natural systems are constructed from structurally distinct and different elements, and so we need to consider multi-agent systems with a diversity of elements. The second principle of the EVS approach is the non-locality of connections between agents. According to this principle an agent could potentially establish communication or other joint activity with any other agent of the population or group. However they cannot establish such connections with everybody simultaneously - we could potentially make contact with any person in the world, but not at the same time (usually). Thus we define the concept of sociability as the maximum number of contacts that an agent could hold an any step of time (Trofimova, 1998a, b).

Probably the assertion of the non-locality of connections between elements inside biological, psychological, social and economical systems is obvious even for a child, and, of course for people inside any society. People interact with one or another member of the environment, groups interact with groups or people and flies interact with all sort of animals. Less obvious non-local interactions occur within cellular communities. The lack of appreciation of this led many mathematicians to the principle of locality of connections between the elements in their models. This locality principle is used in most popular multi-agent models, especially cellular automata (from Ulam, 1962). According to the principle of locality, each agent in these model has already established connections with its neighbors, and the number of such neighbors is very limited (2, 3, 9). Some models, for example neural networks, try to avoid the locality of connections by simply establishing the maximal number of connections: each agent there is connected with every other agent. However these connections are fixed, meaning that the structure of a system is defined a priori and does not change. The results of such modeling have revealed many interesting effects, such as the possibility of producing interesting patterns of connections, including self-reproductive patterns (Gardner, M. 1970), to recognize images (from Rosenblatt, 1962, Minsky & Papert, 1969), to store images and to learn (Samuel, 1959; Holland, 1986; Ackley, Hilton & Sejnowski, 1985, etc.).

The problem is that these phenomena only seem to be similar to actual reproduction, perception and leaning as occurs in living organisms. Cells only seem to be connected solely with their neighbors. Real reproduction never exactly produces the same organism each time; real perception is never free of error (there are always illusions) and real learning never uses the storage of images with equal ranking. I could understand mathematicians who always look at biological, psychological and especially brain structures with baited breath. Sure, nature learned to construct such complex structures with surprising capacities that are difficult to compare with the elementary topological structures that mathematicians are most familiar with. I think that the visual biological structures have misled mathematicians away from the path to adequate modeling.

It is true that some cells, and brain cells too, are connected with each other. But not locally! Each neuron of the adult person has thousands of dendritic connections with other cells and sends axonal branches to thousands more, many of these at considerable distances. The white matter of the brain is solely made up of axons. In addition, neurons can communicate through neurohumoral factors with other neurons and in fact other organ systems such as the immune system. Each neuron swims in an ocean of connections, an enormous space of possibilities for contacts. The same true for somatic cells: connection and regulation between them is not via physical closeness, but through chemical exchange using different kinds of fluid matter that flows through it. If one cell has a special state that can influence another cell (to help, to break, to stimulate, to inhibit, to feed, etc), it is just a question of time (sometimes just milliseconds) for this cell to establish this influence.

The fixed structure of neural networks ( from McCulloch & .Pitts, 1943 till Schwartz, 1990; Arbib, 1995 or Gazzaniga, 1996) is also not very adequate. Such a structure makes all agents potentially involved in the activity of the population level. However real neurons 1) are silent most of time or make random spikes from time to time; and thus do not really participate in the network; 2) the connections between them are not equal as a consequence of the neuron’s communication vehicle (it is not only a question of excitatory or inhibitory types). In point of fact, connections between neurons possess a large variability that allows our brain to code information not only by the morphological structure of connections, but by dynamical patterns in time.

From this point of view we believe that the EVS approach, its principle of flexibility and variability of connections is more adequate for the modeling of activity of natural systems (organisms, groups, organizations or other communities) than traditional neural networks or cellular automata approaches.

The concept of Resources and its use in modeling

We consider the concept of resources broadly: it could refer to energy, matter, chemical elements, time, information, money, service, emotional exchange, and so on. In all of our models we invoke this concept to varying degrees. The agents of the «Compatibility» model receive more life resource for connections with more compatible agents. The agents of the other models could receive, spend, store and grow resource themselves, and so required additional characteristics: the limit of incoming resource (I), the limit of outgoing resource (O), internal resource production (R) and limit to storage (L).

Functional Differentiation (FD) considers functionality as the property of system's units to execute special functions within a system's community. The study of functional differentiation involves understanding the processes whereby a population of individuals, whether humans or cells, economic institutions, species of animals or members of a group in the work place, become specialized in the behaviors which they express. In the case of cells, we see differentiation into blood forming elements, repair elements, control elements, structural elements, and so forth. In the case of humans, we find ourselves drifting into different roles - leader, teacher, healer, mediator, worker, couch potato, etc. Such a specialization reflects certain needs of a system. So if we want to understand and classify specialization of elements inside a system, we have to find parameters that describe these needs.

The existence of a set of indicated resource parameters presupposes some form of partial ordering on the set of possible manifestations of the resource. This might be a material quantification or a functional valuation. Inhomogeneity in the temporal and spatial properties and in the density of the flow induce the differentiation of elements within the system. Thus differentiation of function is a result of the character of a flow passing through a system. (Trofimova, 1999).

In the "Compatibility" model, individual agents attempted to minimize the costs associated with the establishment of cooperative links with neighboring agents. These costs varied according to the 'compatibility' between agents. The links were dynamic, changing with fluctuations in costs. Population size, compatibilities, sociability and contact rate were tunable parameters. The object of study was the formation of connected components.

The study of this model showed that the parameter of sociability plays key role in the phase transition between two types of behavior: (1) participation of an agent in a big cluster, becoming more similar on these cluster characteristics (being social and «like others») and (2) participation in a small, specific cluster (being special and independent). Such a transition leads to the situation where almost all members of the population or group are similar in some «interest» or trait and there is some veto upon different small "groups by interests". It looks like agents become more uniform and controlled by majority of other agents (Fig.1.).

For low populations, this transition bears many of the features of a continuous phase transition. There is a gradual increase in the order parameter across the transition. For large populations, the transition becomes more abrupt. The affiliation shows a very sharp transition from a level near 0 below a critical value, to a level close to 1 above this critical value. Studying different populations and varying different values of sociability parameter (about 300 different runs), we were able to estimate the critical sociability as the function S_c=P^0.6, where P is the population size.

Thus this group dynamic shows the situation of separated small groups hardly having something similar between each other and more easily demonstrating some ignorance toward the main population (for example, in the case of physically separated individuals, or with the low density of population, where we have small sociability) and the effects of the emergence of global system behavior, effects of totalitarian control or the dominance of some idea, image, information over the other internal possibilities of population (that we see in the cases of somebody’s popularity, monopolies in economics, propaganda in mass media, which reaches almost every citizen, or rules inside the organization, etc.)

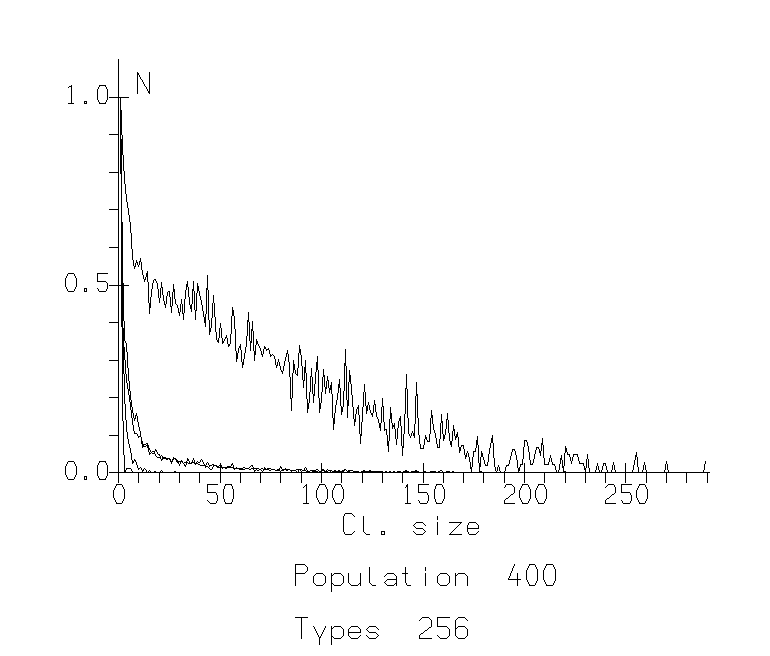Fig. 1a: Cluster Distribution Functions for population 400. The x-axis represents size of clusters, the y-axis represents number of such clusters normalized against the mode. A. Sociability 20

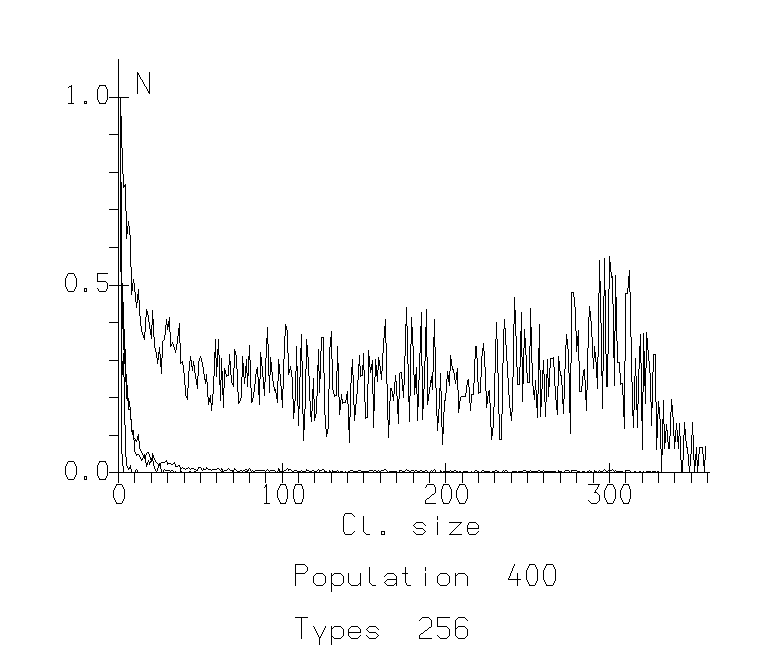Fig. 1b: Cluster Distribution Functions for population 400. The x-axis represents size of clusters, the y-axis represents number of such clusters normalized against the mode. B. Sociability 40

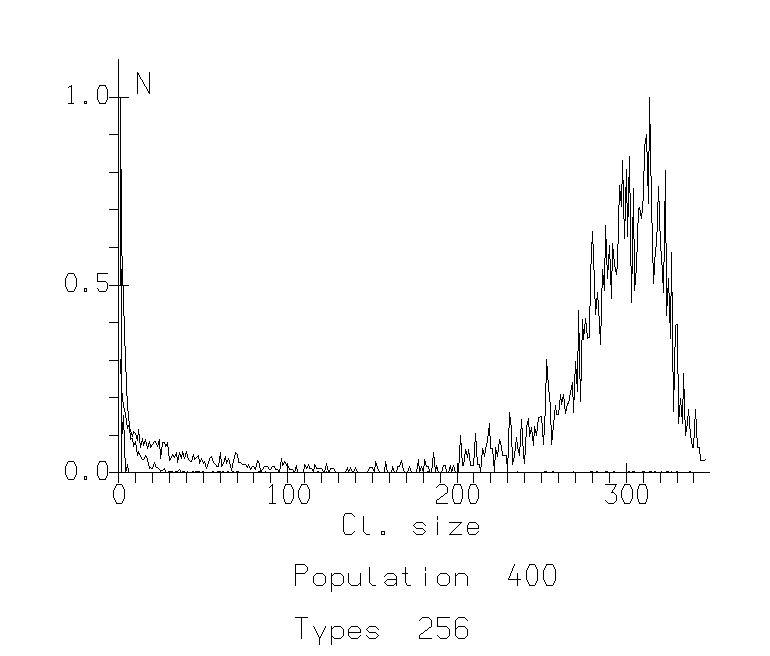Fig. 1c: Cluster Distribution Functions for population 400. The x-axis represents size of clusters, the y-axis represents number of such clusters normalized against the mode. C. Sociability 90

Also we found interesting behavior in the small populations (up to 20 agents). Unlike the middle size (100-500) or large (more then 1000) populations, having structural stability of its dynamics, but very volatile structure of real connections, small populations demonstrated structural stability and very rigid structures of connections. As we looked at the behavior of six different «age» of clusters, usually we could observe that clusters do not live for long times with the same composition, so most of our pictures show the life of the youngest group of clusters. However in the small populations we could see that clusters of different age choose the same totalitarian strategy: even old clusters tend to keep the size, similar to the most unstable clusters (Fig.2). We called it "the effect of small country": there are not big possibilities to change the structure of connections in small isolated communities, so once established customs and groups tend to dominate for a long time over the individual characteristics of members of these communities. Stability of affiliation is connected also with control of diversity of interests, when a element, very different from all community will be forced to follow the characteristics of the big (often single) clusters.

The FD (Functional Differentiation) model shows how inhomogeneity in the flow results in a spreading of properties along selected parameters, resulting in a polarization of abilities within the population of elements. (Trofimova, 1997a). For example, agents with the ability to accept much resource (big I) and spend it (big O) while realizing many contacts with other agents (big sociability S) more often play the function of conductor (in human life they could be journalists, teachers, clerks, postal workers, cashiers, salespeople). A big output of resources (big O) and small input (small I) characterize the producing and disposing sets of functions, while a big I and small O lead to the "condenser" set of functions (leader, selector, "warehouser", inhibitor, etc).

Such a resource description of the roles that people could play in social life vary not with the absolute value of O, I or S that an agent has, but with the ranking that each has inside the population. For example, the real value for an agent of some parameter O could be average in comparison with other populations, but as almost no other has a larger value within this concrete population, this agent will function according to the type with high O.

Other questions were addressed in the "Adaptation" (Trofimova, Mitin, Potapov., Malinetzky, 1997). This model was based upon these ideas and explored the effect of individual differences upon cooperative behaviour in the world of agents, each of which attempted to minimize the costs associated with processing resources through the formation of links with other agents. As in the "Compatibility" model, the agents were given a set of differences a priori, expressed as a vector of traits. However there were two main differences from that model:

1. the individual differences of agents were not abstract traits, but the characteristics of output resource (limit of O; percentage of O derived from the residual of an agent);
2. an agent could change its configuration and become closer to the "average individuality". Each agent attempted to minimize its costs depending upon the degree of similarity in type between itself and those agents with whom it had forged links.

The system was allowed to evolve to stationarity, as every agent could change its behavior. For behavior which was closer to the others, an agent received additional resource, and this, to our mind should lead to complete conformity for all populations. It was conjectured that the system should evolve towards a fixed point attractor, i.e. homogeneity of population, in which all agents have minimized their costs to the same degree. Surprisingly, it appeared that small regions or cluster of cells would persist in which these attributes would continue to fluctuate in a chaotic or possibly periodic manner. In other words, the system was frustrated, indicating symmetry breaking. Thus, even for such a simple model, individual differences persist even in the face of similarity among the majority of the population. This raises a deep question as to whether individual differences are a dynamical necessity.

The model «Resources» extends the «Adaptation» model, as it also examines the situation in which the agent receives a resource depending on its similarity to those with whom connections are established. In the Resource model two variants of structural limits on the connections in a population were offered:

1. The maximum number of connections that an agent can establish with other agents of system is limited, i.e. sociability (like in the previous models). Additionally we decided to check the specifics of an agent’s adaptation process in the inconvenient situation of a deficit of connections. Thus we used the second type of limits on connections:
2. The maximal number of connections in the system. In this case we do not order the personal sociability of agents as before (so agents could establish as many contacts as they want), but the total number of connections in the system is limited and cannot be changed (like at the neural network models).

This model also examined two different variants of an agent’s strategy to choose the connections on each step (criterion of optimization):

• to give preference to connections with agents located closer in the space of the individual characteristics (compatibility strategy, like before); or
• to give the preference to connections that provide greater quantities of a resource then other possibilities (profit strategy; such strategies are popular at the economical models).

We observed the behavior of all these four cases from the point of view of

• adaptation (development of similarity or conformity, unification) process; for it we measured the distances between agents characteristics in the population.
• effectiveness of the work with resources, measuring the total resource of a system;
• group dynamics, measuring the cluster sizes that appear in this dynamics (Trofimova, Mitin, 1998b).

The first qualitative effect, observable in the comparison of all these cases is the influence of a limit on the general number of connections over all populations. It seems that the system does not like the competition of the agents for the connections: the speed of adaptation of elements to each other (their unification) is slower in the case with a limit on the total number of connections. Such systems tend to lose their total resource and do not form groups of connected elements. With such limits agents cannot come to consensus and affiliate with other agents effectively. With the other type of limit (sociability) the distance between elements stabilizes after the normal decrease and occupies a certain value. The system does not lose its resources and lives with group formations (clusters of about 10 or more agents).

Affiliative behavior

First of all the sociability of agents in our models appeared to be the main factor in determining the affiliative behavior, and such behavior appears to be a group effect, independent of the individual characteristics of a subject. It means that the breadth, depth and possibilities for keeping contacts with other agents or groups of agents as allowed in the person's social environment define the development of different kinds of social behavior. We have evidence for the existence of a high level group dynamics which is relatively independent of the low level group dynamics, that is, the behaviour of the individuals, and yet which influences such individual behaviour. Group dynamics has long been viewed as an expression of the behaviour of individuals, averaged over the collective. Here we see that groups possess their own dynamic, independent of the individual. If the individuals making up a large group or population are sufficiently sociable, then they will establish a network of connections within the group which effectively link every individual member to every other. This cohesiveness arises regardless of the degree of similarity among the individuals making up the group, and, as our preliminary evidence shows, paradoxically the greater the diversity among the members, the more readily this coherence is established.

The previous results suggests three scenarios which could generate disorders of "sociability":

1. A person is forced to more social contacts than he (she) can hold in the situation of the high sociability of the population (group). Such a situation happens when a patient is an introvert, living in a large family, or forced into social activity at school, within the community, etc. The same situation can happen when any person has a lack of privacy, whether at home or in the working place. The deficit of privacy leads to a lack of pursuit of individual goals, to more enforced socialization upon the person, and finally to the social regulation of values and interests. From the point of view of the society is it good, as society receives its regulated, socialized, and properly directed member. However on the individual level it might lead to increasing neurosis and depression: a person can feel that his or her individuality did not receive a proper development and appearance, that life was not exactly as desired, that life does not have any personal meaning and value.

   To correct such tendencies we need to reduce the dependence of a person upon obligatory communication and activity, devoted not to this individual's, but to the social group's goals. Both psychological work with a patient and members of his or her reference social group (family or colleagues) should be conducted in order to not eliminate either individual or social priorities.

2. A person has a deficit of contacts in the situation of low sociability (i.e. a diminished possibility to explore and establish many different contacts) in the population. Sometimes we meet this situation, when a patient is an extrovert, living in average town. More frequently it is not only an "extrovert" problem, and the common cases are: 1) children and young people who, according to their age have to test themselves and different life possibilities, have to learn the knowledge about different sides of the world, and 2) elderly people, who gradually lost their circle of communications and business and contact with a much younger society which "doesn't notice" their existence. They may have very little to do in a small town with limited possibilities. Such a situation leads to the creation of artificial and illusory worlds of relations and connections: projections of events and affiliations from the movies, TV-stories, fiction books, leisure activity, etc. Under the condition of deprivation of stimulation in everyday life many kinds of phobias, uncertainty, anxiety, hopelessness, illusions, sleep disorders become more easy to develop for people with sensitive kind of psyche.

   To correct it we need to adapt the patient to the real world, involving him or her in the activity of more distant groups, including work in Internet, rather than by filling out "the hole in sensations" by surrogate images of reality (that decrease a patient's adaptiveness).

3. A special case with affiliation behavior itself is when a person cannot find an appropriate environment that matches his or her interests and needs or has to choose from a narrow circle of contacts, rejecting other wishful connections. The need of a patient in affiliation and identification with a group leads him or her to participation in some group merely because it is available, and not because it is exactly what this patient wants. Such a need in affiliation could indicate family problems or problems with self-identification that a person faces.

   The function that we received could help us to calculate a critical value of sociability, under which we should not expect affiliative behavior on a large big scale (it means more probably many small interacting groups with inconstant members), and attentively study cases when people are devoted too much to some group. Above a critical value of possible contacts and joint activity we should expect an appearance of social control, unification phenomena and some totalitarian tendencies, that also could lead to some psychiatric situations.

Functional behavior

Differentiation of society members by the functional role that they could fulfill usually goes on the basis of a ranking by some abilities that are necessary to conduct this or that function. Usually we are poly-functional, and hold several role positions. The most common disorders, connected with functional differentiation inside human groups are:

1. A person's estimation of their own rank to conduct some functional operation does not match other members' estimations. If the group is wrong, we need mostly psychological work, but if a person has a delusion or psychopathic tendencies, the situation needs some psychotherapy.

2. A person's estimation of his or her possibilities to hold (and conduct) all functions that this person pretends to conduct does not lead to an optimal use of his or her abilities: sometimes too much for one function, sometimes too little for another with the result that the person does not fully realize him or herself. The last case can be mostly psychologically treated, but it is more difficult to deal with than the first one. The person should agree that he or she is no longer good at carrying out some work that this person was involved with, and more critical - that other members of the social environment should accept it and change the arrangement of functional roles.

Using formal modeling, we could find the optimal arrangement in functional differentiation inside a group and so analyze the origin of this or that psychiatric case.

1. Ackley, D.H., Hilton G.E., and Sejnowski, T.J. (1985) A learning algorithm for Boltzman machines. Cognitive Science 9: 147-169.
2. Arbib M.A. (Ed) The handbook of brain theory and neural networks. 1995. MIT Press.
3. McCulloch, W.S. and W.Pitts (1943). A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5: 115-133.
4. Gardner, M. (1970) The Fantastic Combination of John Conway's New Solitaire Game "Life". Scientific American 223 (4), 120-123.
5. Gazzaniga M.S. (Ed) The Cognitive Neurosciences. 1996, MIT Press.
6. Holland J.H. (1986) Escaping Brittleness: The Possibilities of General Purpose Learning Algorithms Applied to Parallel Rule-Based Systems. In R.S.Mishalski, J.G.Garbonell and T.M.Mitchell (Eds.) Machine Learning II. New York: Kauffman. 593-623.
7. Minsky M. & Papert S. (1969). Perceptron: An Introduction in Computational Geometry. Camridge, MA. MIT Press
8. Rosenblatt, F. (1962) Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Washington, D.C.: Spartan Books.
9. Samuel, A.L.(1959) Some Studies in Machine Learning using the Game of Checkers. IBM J.Res.Dev. 3, 210-229
10. Schwartz E.J. (Ed.) Computational Neuroscience. 1990. MIT Press. Pp.46-55.
11. Sulis W. Causality in Naturally Occurring Computational Systems. 1994. World Futures. 39, 225.
12. Trofimova I. (1997a). Functional Differentiation in Developmental Systems. In: Complex Systems. Proceedings of the International Conference. Oxford. In press.
13. Trofimova I., Mitin N., Potapov A., Malinetzky G. (1997b). «Description of Ensembles with Variable Structure. New Models of Mathematical Psychology». Preprint N 34 of KIAM RAS.
14. Trofimova I. (1998a). From living systems to synergetic models and back. In: Synergetics. Proceedings of a workshop. Vol. 1. Moscow, MSU Press, pp.69-80. (In Russian).
15. Trofimova I. (1998b). The definition of parameters for measurement in psychology. In: F.M. Guindani & G. Salvadori (Eds.) Chaos, Models, Fractals. Italian University Press. Pavia, Italy
16. Trofimova I., Mitin N. (1998) Modeling of Group Interactions: Some Useful Concepts. Proceeding of the Conference Managing the Complexity, Toronto. In press.
17. Trofimova I., Potapov A., Sulis W. (1998).«Collective Effects on Individual Behavior: In Search of Universality». Chaos Theory and Applications. Pp.35-45.
18. Trofimova I. (1999) Ensembles with Variable Structure (EVS) in the Modeling of Diversity Phenomena. Submitted to: Complexity.