Invited Symposium: Hypertension III: Flow-Induced Vascular Remodeling
| INABIS '98 Home Page | Your Session | Symposia & Poster Sessions | Plenary Sessions | Exhibitors' Foyer | Personal Itinerary | New Search |
INTRODUCTION
Vascular beds are designed to optimally supply oxygen to tissue while coping with a number of challenges, amongst others of mechanical origin. Thus, blood pressure results in a wall stress that needs to be carried by contractile and elastic filaments in the wall. Likewise, flowing blood exerts a shear stress on the endothelial lining. The design may be the result of evolution, i.e. have a genetic base, in combination with structural adaptation processes driven by wall stress and shear stress. The design includes the ability for wall stress and shear stress driven functional responses: respectively the myogenic response and flow-dependent dilation.
This contribution aims to provide some general considerations when trying to understand the role of acute and structural responses to flow and pressure in the adaptation of vascular networks. These considerations are based on two interaction schemes: Fig. 1, which depicts a single vessel, and Fig. 2, which indicates the hemodynamic interactions between multiple vessels within a network.
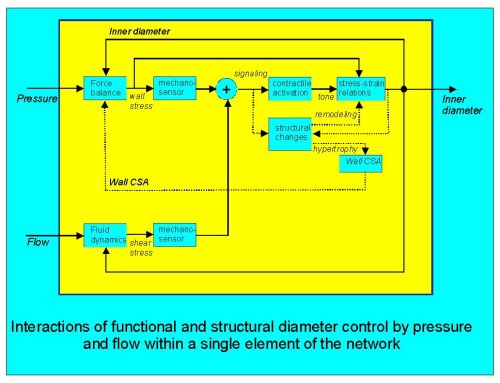 Fig. 1: a conceptual scheme of the interactions that could occur in the functional and structural responses to pressure and flow in a single segment. Dashed lines indicate structural effects.
Fig. 1: a conceptual scheme of the interactions that could occur in the functional and structural responses to pressure and flow in a single segment. Dashed lines indicate structural effects.
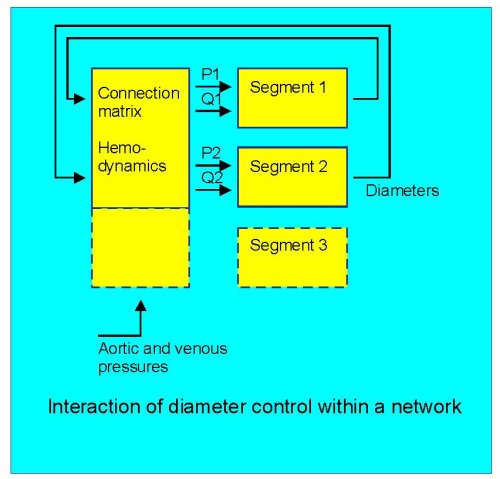 Fig. 2: a conceptual scheme of diameter effects on local pressure and flow, shown for two segments.
Fig. 2: a conceptual scheme of diameter effects on local pressure and flow, shown for two segments.
THREE CONSIDERATIONS
First, functional and structural responses to mechanical stimuli interact. For a given pressure step, the acute response is myogenic tone development, resulting in constriction and thereby a smaller elevation of the wall stress. If this control loop were to have a very high gain, wall stress would be independent of the pressure, and there would be no obvious need for stress-driven structural changes. Yet, myogenic stress control is generally not perfect and accordingly a stimulus for structural changes does occur. In turn, the structural response affects the myogenic response: hypertrophy reduces wall stress, while remodeling (defined here as a shift in active and/or passive stress-strain relations) also affects the consequences of alterations in tone on diameter. A further possible interaction may result from an effect of the diameter on structural changes: would a long-lasting vasodilation eventually result in structural widening simply because newly formed elastic and contractile fibers have their resting or optimal length matched to the dilated diameter?
Secondly, for a single segment (Fig. 1) flow and pressure responses interact: both signals have to be combined at some point (here denoted by the circle) in order to result in a single functional response and possibly a single initiation of structural responses (pro-oncogene expression, phenotype modulation). Apart from these cellular interactions, for a given pressure and flow the shear stress response increases the wall stress (Laplace) and vice versa (third power dependancy of shear on diameter). Thus, there is a clear mechanical interaction.
Thirdly, vessels operate in a network (Fig.2). Consequently, the responses of any segment to pressure or flow influences the pressure and flow for that segment as well as all others. These influences critically depend on the connection matrix of the segments. The network behaviour may not be easy to predict from the responses of individual vessels. As an exmple, it is easily shown that vascular adaptation to only shear stress is a stable process in models of single vessels, resulting in a third-power dependency of diameter on flow (Q =c×d3). This third-power law implies that diameters in mother and daughter vessels also are related by their third powers, and indeed this appears to be the case when studying branching patterns, although exceptions exist (VanBavel and Spaan, Circ Res 71:1200-1212, 1992). The third-power relation also has been considered optimal in terms of cost functions associated with perfusion (Murray, PNAS 12:207-214,1926), and based on the single vessel shear stress response it is tempting to speculate that shear stress adaptation is a mechanism for optimization of vascular diameters. However, models of complete networks equipped with this adaptation rule show massive rarefaction and end up as a single preferential channel (Hacking et al, Am J Physiol 270: H364-H375, 1996). Thus, shear stress alone can not be sufficient to control growth of vascular networks.
CONCLUSIONS
All these interactions (let alone the interactions with non-mechanical factors) seem complicated, and it is tempting to restricts one's focus to a single aspect (only functional or only structural, or isolated vessel studies without consideration of network properties). However, a true understanding of local flow control needs an integrative approach. The challenge for the coming years will be to translate conceptual schemes such as both figures in this contribution to complete, quantitative integrative models. Due to the complexity of such models, this can no longer be done by one or a few labs, and, in the spirit of the physiome project, needs also an integration of information provided by all labs working on the matter.
| Discussion Board | Previous Page | Your Symposium |