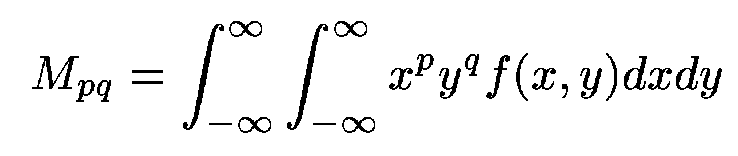Poster
Contents
| INABIS '98 Home Page | Your Poster Session | Related Symposia & Posters | Plenary Sessions | Exhibitors' Foyer | Personal Itinerary | New Search |
in Diabetic Retinopathy
Introduction
The study of the retinal vessels plays a crucial role in many clinically relevant diseases such as systemic hypertension, arteriosclerosis and diabetes. In particular, diabetic retinopathy is the leading cause of new adult blindness. Thought diabetes can affect the eye in a number of ways, the fine network of blood vessels in the retina is usually involved - hence the term diabetic retinopathy.
The blood vessel changes that occur in retinopathy are not visible without special instruments. Modern imaging devices such as the Scanning Laser Ophthalmoscope (SLO) [1], in combination with computer analysis make the observation of the capillary macular network possible [2,3,4,5].
In this work a computational approach for detecting and quantifying diabetic retinopathy is proposed. Particular attention has been paid to the study of Foveal Avascular Zone (FAZ). In fact, retinal capillary occlusion produces a FAZ enlargement. Moreover, the FAZ is characterized by qualitative changes showing an irregular contour with notchings and indentations [6].
On this ground, our aim was the development of an automatic system for the quantitative morphological evaluation of the vascular lesions of the fundus oculi occurring in diabetic subjects. The study is mainly focused on the analysis of the FAZ (the degree of its enlargement and its shape change) and on the extraction of a proper set of features to quantify FAZ alterations in diabetic patients.
In order to extract such parameters, first we used an automatic segmentation procedure to correctly identify the FAZ boundary [7], then we referred back to the theory of moments to obtain a reliable quantitative description of FAZ shape.
Materials and Methods
In this study 12 diabetic subjects and 14 healthy subjects were considered. Demographic and clinical data of the two groups of subjects are reported in Table 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 1: Demographic and clinical data of diabetic and control
subjects.
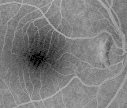
Retinal images were taken by a SLO, with a frequency of 25 frames per second following the injection of a bolus of fluorescein. These images were digitized into 512 × 512 pixel matrices with 256 gray levels per pixel. The retinal region is approximatly 20 × 20 degrees. An example of original image can be seen in Figure 1
Click to enlargeFigure 1: SLO image of ocular fundus:
the darker region is the macula and
the lighter structures are the
retinal blood vessels.
Such images were first preprocessed by an enhancement technique and then segmented with an automatic procedure. Such techniques are presented in detail in previous papers [7,8,9,10,11] and will not be discussed here.
Examples of FAZ shapes obtained are reported in Figure 2.
Click to enlargeFigure 2: Examples of FAZ shapes:
n1, n2, n3, n4, n5, n6 = normals;
d1, d2, d3, d4, d5, d6 = diabetics.
As pointed out by ophthalmologists, the considerable variability of the FAZ dimensions made size-based diagnostic criteria of FAZ abnormalities in diabetic patients difficult [6].
For example, the cases (n3) and (d2) of Figure 2 have almost the same dimensions, but they have a different orientation. Moreover, the case (d5), which could be classified as normal based on size and orientation, shows a very irregular outline and has a larger boundary then the normal case.
Quantitative measurements reported in the clinical literature (such as circumference, area, longest diameter, longest perpendicular diameter) alone, are not complete descriptors of FAZ shape useful for a correct identification of diabetics. On the other hand, ophthalmologists rely on a qualitative description of the FAZ to detect the presence and assess the severity of diabetic retinopathy [6].
This prompted us to experiment with different representations which could be able to provide a better characterization of FAZ outline. In particular, we tried to extract features which can capture not only the size of the object, but also its shape and spatial orientation.
The theory of moments [12,13,14] provides an
interesting and useful way for representing the shape of objects.
The geometric moments {Mpq}
are given by
where p,q = 0, 1, 2, ...,
,
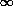and f(x,y) is the image intensity
function which is assumed piecewise continuous and with a bounded
support.
For a digital (M × N) image,
the double integration of Mpq
in (1) is usually approximated by a double summation
 |
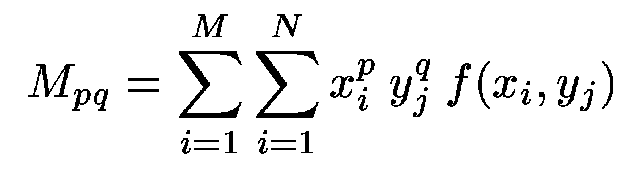(2) |
>From Mpq one can compute the central moments
,
defined as
 |
(3) |
where
 |
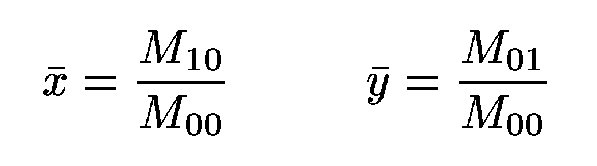(4) |
It is worth noting that {µpq} are invariant with respect to image translation.
According to the properties of lowest order moments[12] ,
we propose the use of the following set of central moments:
 |
(5) |
We observed that higher order moments have, in general, increasingly smaller magnitude, and can be neglected (this is equivalent to truncating the series and to keeping an approximation of f(x,y)). It is well known that, in principle, most of the image information can be recaptured by using a sufficiently large number of a particular set of image moments.
Several types of moments have been investigated [12] to derive a set of invariants with the property of being invariant under image translation, scaling and rotation. In our case, we propose the use of a set of central moments, which are invariant only under image translation, because size and orientation are important diagnostic features.
The geometric interpretation of the lower order central moments for a region R shows they have a direct analogy with the mechanics of bodies. Such descriptors can be interpreted as listed below:
- µ20 horizontal centralness
- µ02 vertical centralness
- µ11 diagonality; indication of quadrant with respect to centroid where R has more mass
- µ12 horizontal divergence; indicates the relative extent of the left of R compared to the right
- µ21 vertical divergence; indicates the relative extent of the bottom of R compared to the top
- µ30 horizontal imbalance; location of the center of gravity with respect to half horizontal extent
- µ03 vertical imbalance; location of the center of gravity with respect to half vertical extent
It must be pointed out that moments can be classified as:
- region moment
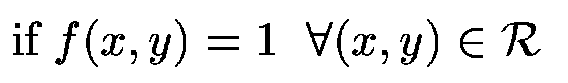
(6)
- boundary moment
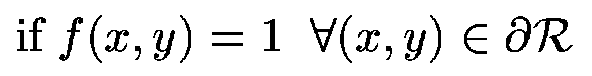
(7)
and 
denote respectively a region and its boundary.
In addition to the size, region moments capture important shape characteristics such as orientation and elongation (i.e. how much the area is concentrated along a particular axis). These features are usually evaluated only qualitatively by physicians, observing the ocular fundus.
Boundary moments provide useful information related to the shape contour, its degree of regularity and its tortuosity, referred by ophthalmologists as ``erosion'' of the FAZ outline.
As boundary moments tend to capture contour features better than region moments, we decided to use both of them. In this way, the adopted descriptor set includes a sub-set of shape characteristics (region moments) mainly related to the orientation and size of the FAZ, along with a sub-set of boundary characteristics (boundary moments) which are expected to provide useful information in the case of diabetic retinopathy. In fact, such a disease is usually related to a quite irregular FAZ contour.
Results
To assess the utility of moment features they were used to classify diabetic and non diabetic subjects. Discrimination between normal and diabetic subjects was achieved by using a back-propagation neural networks.
We observed that the µ02 and µ03 parameters are less significant, while µ11, µ12 and µ21 are more significant. In fact, they are able to better characterize shape asymmetries, and this confirms the qualitative observations that can be found in the medical literature.
Although potentially more sensitive to noise, the boundary moments appear to be more suitable for describing the irregularities of the FAZ.
Classification results were evaluated with the leave-one-out method, results obtained on the feature set based on region and boundary moments respectively are reported in Table 2 and 3.