By 'short eyes' we shall understand eyes with axial lengths <= 22 mm. From a database survey covering biometry data of 15124 cataract eyes it was found [2] that the short eye percentage amounted to 11.1 % (cf Tab.1).

--------------------------------------------------------------------------------
axial length range [mm]            AL <= 22       22 < AL < 25       AL >= 25
--------------------------------------------------------------------------------
anterior chamber   AC [mm]           2.69             3.14             3.48
lens thickness     LT [mm]           4.69             4.46             4.40
axial length       AL [mm]          21.44            23.27            27.09
corneal radius     RC [mm]           7.45             7.69             7.76

total              n                1 678           11 812            1 633
percentage         %                 11.1             78.1             10.8
--------------------------------------------------------------------------------

Fig.1 shows a typical immersion A-scan of such an eye with an axial length of 19.2 mm. It has a thick lens (4.9 mm) and a shallow anterior chamber (2.0 mm).

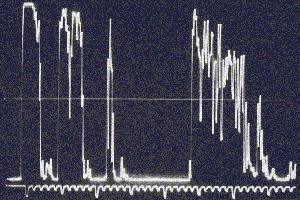Fig.1: Typical immersion A-scan of a short eye with anterior chamber depth AC=2.0 mm, lens thickness LT=4.9 mm and axial length AL=19.2 mm.

Immersion scanning is to be preferred for axial length measurements, especially for short eyes. First, with the corneal double peak echo clearly discernible, all 4 ocular landmark echoes (cornea, lens front and rear, back wall) may be adjusted for optimal steepness thus achieving best orientation; second, no danger of indenting the globe exists thus preventing the axial length from being measured too short which would later result in a postoperative myopization.

Problems may also arise from some A-scan units which - in automatic biometry mode - might not expect an anterior chamber as shallow and/or a lens as thick. The measurement may be rejected or even faulty. Manual mode has to be selected in this case. Another source of errors is found in the use of a mean sound velocity instead of individual velocities for each ocular compartment. A thick lens will lead to an underestimation of the axial length. For example, with a popular setting of 1550 m/s, the axial length of Fig.1 would be given as 19.1 mm instead of 19.2 mm.

Due to the small anatomical dimensions, ultrasonic measurements are generally more sensitive to systematic measurement errors. In addition, different A-scan devices may produce different axial length results as a consequence of the individual technical design features of each instrument. The same holds for the determination of corneal power by keratometry or corneal topography. Starting from curvature data, different keratometer indices are used for the conversion into corneal refractive power. A 7.5 mm radius, e.g. will translate into 44.3 dpt with an index of 1.332 (Zeiss keratometer), whereas the keratometer index (1.3375) of widely used popular Javal type instruments had been deliberately choosen to give a corneal power of 45.0 dpt for this very radius.

So, apart from being more difficult to obtain, short eye parameters are very sensitive to the measurement setup, i.e. the biometry and keratometry devices used for their acquisition.

The intraocular lenses to be used for short eyes must usually have high dioptric powers (30 dpt or more). Commonly, these powers are not readily available and the lenses themselves must be especially designed and manufactured. With high-powered lenses a new problem starts to rise: differences between total power and vertex power may not be neglected any more. Due to still different power-labelling policies of IOL manufacturers, the diopter value for a given lens may either denote total or back vertex power. Powers relate to the effective focal length (f', principal plane to focal point) for total power and to vertex distance (back vertex to focal point) for vertex power. To make things worse, these distances are dependent on the shape of the lens optic (cf. Fig.2).

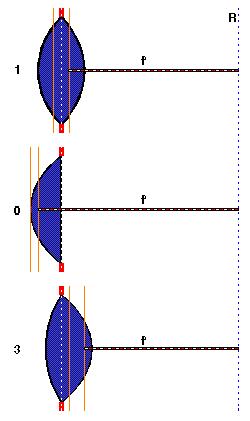Fig.2: Principal planes of lenses of different shape: 0: convex-plano, 1: biconvex with 1:1 ratio of anterior to posterior lens radius; 3: biconvex with 3:1 ratio.
All lenses are situated in the same position (e.g. capsular bag). In order to focus onto the retina R, each lens must have a different focal length f', i.e. different power.

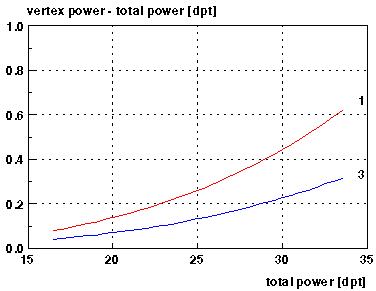Fig.3: Difference between vertex power and total power vs total power for theoretical lenses (PMMA, 7 mm optic) #1 and #3 of Fig.2. The image principal plane of the asymmetric lens #3 is closer to its back vertex than for the equiconvex lens #1, thus, the difference between vertex and total power is smaller than for lens #1 (cf. Fig.2).

From Fig.3 it can be seen, that for a total power of about 30 dpt these differences may reach nearly half a diopter for a biconvex IOL with a 3:1 radius ratio. So, two given lenses with the same power label may optically behave completely different. Another geometry related effect can also be seen from Fig.2: intraocular lenses of different shape, positioned at the same location require different focal lengths i.e. different powers. An additional aspect worth noting is the fact that high dioptric lenses literally are 'thick' lenses. IOL formulas, however, with the exception of empiric algorithms like SRK I/II, are valid mathematically only for (infinitely) 'thin' lenses.

If the above described effects due to different biometry methods (applanation, immersion), different keratometer calibrations und IOL related effects are combined for a short eye of 21 mm, refractive errors of up to 2.4 dpt may result [3]. Half of this error can be attributed to IOL specifications.

How can all of these factors be made allowance for in a given clinical surrounding ? The total of the individual biometry and keratometry intruments as well as the specifications of the individual lens type used must be reflected in individualized lens constants. For the SRK II (see e.g. [4]) and SRK/T formula [5], the constant to be individualized is the A-constant. Although, as has been pointed out earlier, SRK II (and even more SRK I) should not be used any longer - especially not for short eye calculations, this formula is still very popular. The lens constant of theoretical formulas is related to the optical ACD and comes as ACD-constant, surgeon factor (in the HOLLADAY formula) or personalized ACD (in the HOFFER Q). Theoretical formulas are based on geometrical thin lens optics and are of the form (see e.g.[6]):

                       n          n                          
                DL = -----  -  -------                         
                     L - d     n/z - d                         
                                                               
                    ref                       nC - 1        
with   z = DC + -----------     and     DC =  ------        
                1 - ref dBC                      RC        

DL  : IOL power
DC  : corneal power
RC  : corneal radius
nC  : keratometer index
dBC : vertex distance between cornea and spectacles
ref : desired refraction
d   : optical ACD
L   : axial length
n   : refractive index of aequeous and vitreous (1.336)

Theoretical formulas differ among each other by the individual recipes how biometric and keratometric measurement data should be translated into the parameters L, d and DC of the above basic formula.

Individualizing constants is equivalent to adjusting them so as to produce a mean zero prediction error for not too small a data set of postoperative refractions. Instead of carrying out the optimization for all axial lengths, better results may be obtained by using a triple individualization for short, normal and long eyes ([7],[8]).

Another approach - advocated by us - is to use 3 constants a0, a1 and a2 in combination with the preop ultrasonically measured ACD in order to predict the axial length dependence of the optical ACD (cf e.g. [6]). Tab.2 summarizes some results of triple individualization for a silicone IOL.

--------------------------------------------------------------------------------
axial length range [mm]            AL <= 22       22 < AL < 25       AL >= 25
--------------------------------------------------------------------------------
anterior chamber    AC [mm]          2.80             3.26             3.58
axial length        AL [mm]         21.76            23.38            25.56
corneal radius      RC [mm]          7.47             7.73             7.83
total               n                   6               98               14

A-constant for SRK II               120.7            119.8            118.7
A-constant for SRK/T                119.6            119.3            119.2
--------------------------------------------------------------------------------

--------------------------------------------------------------------------------
Haigis constants                  a0=2.137        a1=-0.026         a2=0.133
--------------------------------------------------------------------------------

With this concept, significantly different prediction curves for the optical ACD are obtained in Fig.4 for the three IOL models of Fig.2. For this calculation, an axial length dependent eye model has been used ([9],[10],[11]).

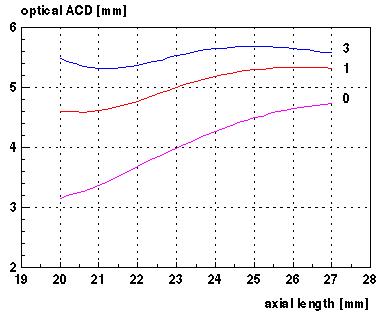Fig.4: Optical ACD vs axial length for theoretical eye model and 3 model lenses (PMMA, 7 mm optic). Lens annotations as in Fig.2.

To improve the quality of IOL calculation in general and especially in short eyes, patients have to be followed up and their stable postoperative refractions have to be measured. These values are then taken to improve the (triple) individualization of lens constants. Thus, with every new patient, the results will get better and more predictable.

We retrospectively analyzed the results of IOL implantations in patients with short eyes (AL <= 22 mm) and shallow anterior chambers. Among them were 9 cases without glaucomatous history respectively no optic disc damage and no loss of visual field. 3 patients were suffering from chronic angle glaucoma, 4 had a history of acute angle closure and 11 eyes showed a primary open angle glaucoma with narrow angle. The biometric findings for these patients are compiled in Tab.3.

--------------------------------------------------------------------------------
grp n      AC [mm]       LT [mm]        AL [mm]        LT/AL           AC/LT
--------------------------------------------------------------------------------
1   9   2.03 ± 0.22   5.15 ± 0.61   21.33 ± 0.43   0.241 ± 0.028   0.404 ± 0.086
2   3   2.02 ± 0.06   5.51 ± 0.34   21.39 ± 0.04   0.257 ± 0.015   0.368 ± 0.032
3   4   1.79 ± 0.14   5.61 ± 0.42   21.08 ± 0.76   0.266 ± 0.014   0.323 ± 0.050
4  11   2.18 ± 0.23   5.29 ± 0.55   21.82 ± 0.58   0.242 ± 0.026   0.421 ± 0.087
--------------------------------------------------------------------------------

It is well known that lens thickening with age contributes to the possibility of angle closure glaucoma ([12], [13]). WOLLENSAK et al. [13] observed the mean lens thickness in angle closure glaucoma to be 0.5 mm greater than in normal eyes. We found a mean difference of +0.32 mm in lens thickness between eyes with acute angle closure glaucoma and primary open angle glaucoma and a value of +0.22 mm for the difference between chronic closure glaucoma and primary open angle glaucoma.

The lens thickness/axial length factor LT/AL (LAF) which is mentioned in literature as an indicator for potential risk of angle closure (>0.229) ([12],[13],[14]) was higher in all our groups (between 0.241 (normal and primary open angle glaucoma) - 0.266 (acute angle glaucoma)). This may be due to the small sample numbers and the extremely short eyes of our groups.

The ratio AC/LT between the anterior chamber and the lens thickness was 0.323 in those eyes which had already suffered an acute angle closure attack. Chronic closure glaucoma eyes showed this ratio to be 0.368, whereas normal (0.404) and glaucomatous eyes without a closure history (0.421) presented with a higher ratio. Again, the statistical significance out of such small samples is questionable.

The patients of groups 1 - 4 were supplied with 11 RAYNER 755U lenses and 10 memory lenses type MENTOR U940A. The prediction errors of postoperative refraction (true refraction - calculated refraction) for these cases is summarized in Tab.4.

--------------------------------------------------------------------------------
                                              true - calculated refraction [dpt]
grp          IOLs implanted                   optimized                  default
--------------------------------------------------------------------------------
1            5 x RAYNER 755U                  +0.47 ± 0.62          -0.19 ± 0.57
2            3 x MENTOR U940A                   no useful refraction measurable
3            2 x RAYNER 755U                  -0.48 ± 1.25          -0.96 ± 1.28
             2 x MENTOR U940A                 -2.14 ± 1.50          -2.09 ± 1.44
4            4 x RAYNER 755U                  -0.09 ± 0.67          -0.78 ± 0.61
             5 x MENTOR U940A                 -0.05 ± 1.03          -0.58 ± 0.95
--------------------------------------------------------------------------------

Refraction was calculated using the manufacturer's constant (755U: A=118.0, 940A: A=119.0, denoted by 'default' in Tab.4) as well as the optimzed constants a0, a1, a2 ('optimized' in Tab.4), which were derived earlier from the stable postoperative refractions of two different patient groups (n=13 for MENTOR U940A, n=83 for RAYNER 755U). The individual axial length dependences of the optical ACDs of the 2 lenses are depicted in Fig.5. The different axial length behaviour is clearly visible.

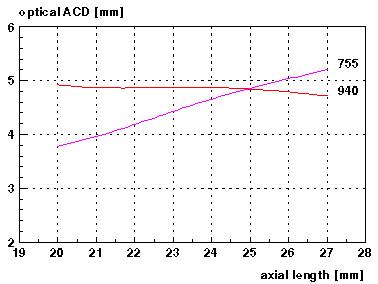Fig.5: Optical ACD vs axial length for theoretical eye model and real lenses RAYNER 755U (755) and MENTOR 940A memory lens (940).

Although, as already mentioned, the group totals are rather small, an optimization effect can clearly be seen in group 4 (cf. Tab.4).

In general, without individualization of constants, the calculated refractions tended to be more myopic.

For more reliable results, the number of followed up patients with short eyes and glaucoma conditions has to be increased. This is done in a continuing study.

The short eye problem in IOL calculation has been reviewed with respect to biometry and keratometry related aspects. Special allowance has been made for effects due to the IOL, which have not yet found a broad attention in the ophthalmic community. To overcome the short eye problem, the axial length dependence of the optical ACD has to be taken into account. This may be done by using multiple IOL constants which have to be optimized for the individual clinical working and measurement setup. The optimization process was demonstrated for 27 eyes with axial lengths <= 22 mm and shallow anterior chamber. Without optimization, all eyes would have become more myopic. Acute angle closure glaucoma eyes could not be analyzed due to unmeasurable refraction; chronic angle closure glaucoma patients remained more myopic in spite of the lens constant optimization. Primary open angle glaucoma patients with narrow angle gained most, since the prediction error in their group was negligible. The results, however, suffer from their small sample numbers. Therefore, further studies are necessary to shed more light on short eyes, especially on those with glaucoma conditions.